奇异值分解

奇异值分解¶

本 notebook 介绍了用于奇异值分解的 da.linalg.svd 算法

启动 Dask Client 以查看仪表板¶

启动 Dask Client 是可选的。它将提供一个仪表板，有助于了解计算过程。

仪表板链接将在您创建 client 后显示。我们建议您在一侧屏幕打开仪表板，同时在另一侧使用 notebook。这可能需要一些精力来排列窗口，但同时查看两者对于学习非常有帮助。

[1]:

from dask.distributed import Client, progress
client = Client(processes=False, threads_per_worker=4,
                n_workers=1, memory_limit='2GB')
client

[1]:

Client

Client-8ad1cc86-0de1-11ed-a4f6-000d3a8f7959

连接方法： Cluster 对象	集群类型： distributed.LocalCluster
仪表板： http://10.1.1.64:8787/status

集群信息

LocalCluster

9a88c089

仪表板： http://10.1.1.64:8787/status	工作节点 1
总线程数 4	总内存： 1.86 GiB
状态：运行中	使用进程： False

调度器信息

调度器

Scheduler-ad8714da-ab0d-4c50-a4cb-ec68028ac54d

通讯： inproc://10.1.1.64/9462/1	工作节点 1
仪表板： http://10.1.1.64:8787/status	总线程数 4
启动时间：刚刚	总内存： 1.86 GiB

工作节点

工作节点：0

通讯： inproc://10.1.1.64/9462/4	总线程数 4
仪表板： http://10.1.1.64:39957/status	内存： 1.86 GiB
Nanny：无
本地目录： /home/runner/work/dask-examples/dask-examples/machine-learning/dask-worker-space/worker-we6_wppm

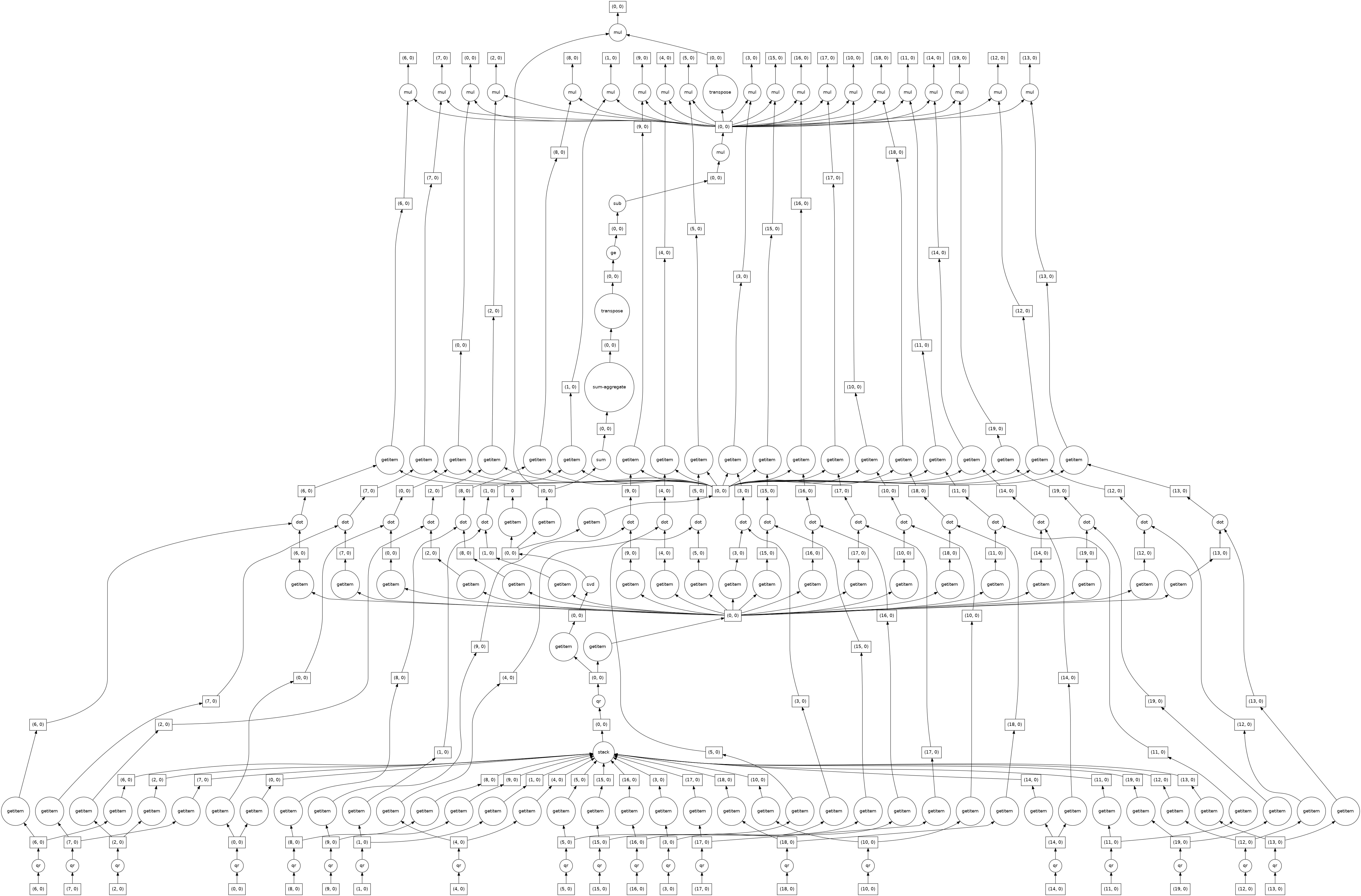
计算高瘦矩阵的 SVD¶

对于许多应用，提供的矩阵行数远多于列数。在这种情况下，可以使用专门的算法。

[2]:

import dask.array as da

X = da.random.random((200000, 100), chunks=(10000, 100)).persist()

[3]:

import dask

u, s, v = da.linalg.svd(X)
dask.visualize(u, s, v)

[3]:

[4]:

v.compute()

[4]:

array([[ 0.09994831,  0.10007229,  0.09997617, ...,  0.09995264,
         0.09995591,  0.09984163],
       [ 0.05585195, -0.06184545, -0.04747733, ..., -0.06275421,
        -0.2061527 ,  0.18218227],
       [ 0.01277435,  0.00484692, -0.04387551, ...,  0.00444605,
         0.12143905, -0.06438531],
       ...,
       [ 0.02933106,  0.00834248,  0.0103009 , ..., -0.06069817,
         0.01291796,  0.12832988],
       [ 0.0901224 , -0.00492353, -0.00470015, ...,  0.14196305,
        -0.09734339, -0.05803211],
       [ 0.16619815,  0.14906927, -0.18081339, ..., -0.1346468 ,
         0.12524437,  0.01322112]])

使用近似算法计算一般非瘦矩阵的 SVD¶

当列中也有许多分块时，我们使用近似随机算法来仅收集少数奇异值和向量。

[5]:

import dask.array as da

X = da.random.random((10000, 10000), chunks=(2000, 2000)).persist()

[6]:

import dask

u, s, v = da.linalg.svd_compressed(X, k=5)
dask.visualize(u, s, v)

[6]:

[7]:

v.compute()

[7]:

array([[ 0.00997573,  0.01011564,  0.00997098, ...,  0.00998413,
         0.00994515,  0.0099736 ],
       [-0.00048293,  0.00247921, -0.00527027, ..., -0.00606932,
        -0.01272348,  0.00818248],
       [ 0.00145378, -0.00278148,  0.01078658, ..., -0.00428512,
        -0.00213905, -0.00738961],
       [-0.00984979, -0.00230993, -0.00277437, ...,  0.0056367 ,
        -0.00199535, -0.01409744],
       [-0.00210629, -0.00320545, -0.00190336, ...,  0.01871436,
        -0.01494592, -0.00274385]])

前一个

广义线性模型

下一个

分析网络托管的 JSON 数据

Dask 示例文档